LV015-AES基本原理

参考：
Advanced Encryption Standard (AES)
高级加密标准 AES-FIPS197 中文版

一、基础知识

1. 输入和输出

AES 算法的输入和输出均为一个长度为 128 的比特串（值为 0 或 1）。这些序列也可以称为分组(blocks)，其中含有的位(bits)数也称为分组长度。

AES 算法的密钥是 128,192 或 256 比特的序列。AES-FIPS197 标准中不允许其它的输入、输出长度和密钥长度。序列中比特的编号从 0 开始，至序列长度(分组长度或密钥长度)减 1。将该比特的编号 i 称为其索引。根据分组长度和密钥长度决定其值属于下列范围中的哪一个： $0 \leq i < 128$ , $0 \leq i < 192$ 或 $0 \leq i < 256$ 。

AES 加密过程涉及到 4 种操作，分别是字节替代、行移位、列混合和轮密钥加。解密过程分别为对应的逆操作。由于每一步操作都是可逆的，按照相反的顺序进行解密即可恢复明文。加解密中每轮的密钥分别由初始密钥扩展得到。

2. 状态(State)

AES 算法的运算都是在一个称为状态的二维字节数组上进行。一个状态由四行组成，每一行包括 Nb 个字节，Nb 等于分组长度除以 32。用 s 表示一个状态矩阵，每一个字节的位置由行号 r (范围是 $0 \leq 0 < 4$ )和列号 c (范围是 $0 \leq c < N b$ )唯一确定，记为 $s_{r, c}$ 或 $s [r, c]$ 。在 AES-FIPS197 标准中 Nb = 4，即 $0 \leq c < 4$ 。

在加密和解密的初始阶段将输入字节数组 $i n_{0}, i n_{1}, . . ., i n_{15}$ 复制到如图所示的状态矩阵中。加密或解密的运算都在该状态矩阵上进行，最后的结果将被复制到输出字节数组 $o u t_{0}, o u t_{1}, . . ., o u t_{15}$ 。

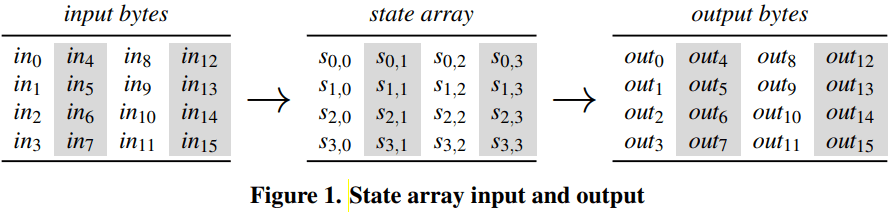
在加密和解密的初始阶段，输入数组 in 按照下述规则复制到状态矩阵中：

s [r, c] = i n [r + 4 c] f o r 0 \leq r < 4 且 0 \leq c < N b

在加密和解密的结束阶段，状态矩阵将按照下述规则被复制到输出数组 out 中：

o u t [r + 4 c] = s [r, c] f o r 0 \leq r < 4 且 0 \leq c < N b

3. 加解密函数

设 AES 加密函数为 E，则

C = E (K, P)

其中 P 为明文，K 为密钥，C 为密文。也就是说，把明文 P 和密钥 K 作为加密函数的参数输入，则加密函数 E 会输出密文 C。

设 AES 解密函数为 D，则

P = D (K, C)

其中 C 为密文，K 为密钥，P 为明文。也就是说，把密文 C 和密钥 K 作为解密函数的参数输入，则解密函数会输出明文 P。

二、AES-128 算法流程

AES 128 的整体结构如下图所示，其中的 W[0:3]是指 W[0]、W[1]、W[2]和 W[3]串联组成的 128 位密钥。上面说到，AES 的加密公式为

C = E (K, P)

在加密函数 E 中，会执行一个轮函数，并且执行 10 次这个轮函数，加密的第 1 轮到第 9 轮的轮函数一样，只有第 10 次有所不同。前 9 轮中，每轮包括 4 个操作：字节代换、行位移、列混合和轮密钥加。也就是说，一个明文分组会被加密 10 轮。

AES 的核心就是实现一轮中的所有操作。由于每一步操作都是可逆的，按照相反的顺序进行解密即可恢复明文。最后一轮迭代不执行列混合。另外，在第一轮迭代之前，先将明文和原始密钥进行一次异或加密操作。

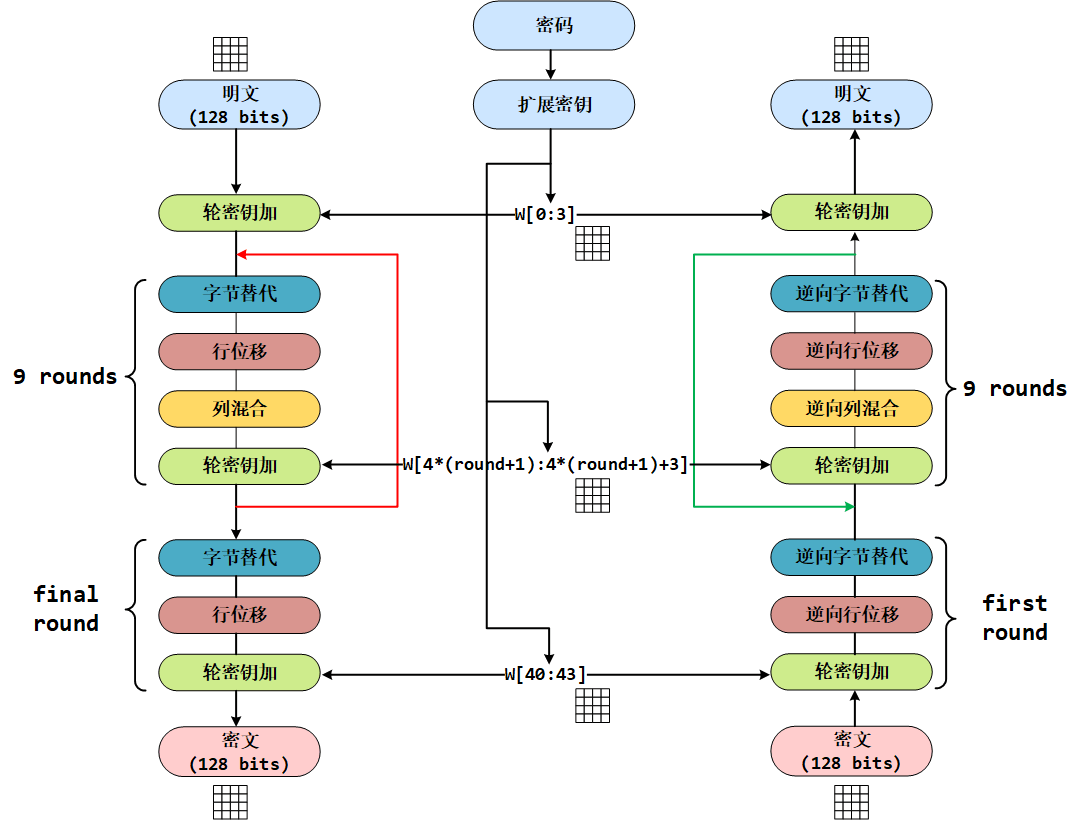
加解密中每轮的密钥分别由初始密钥扩展得到。算法中 16 个字节的明文、密文和轮密钥都以一个 4x4 的矩阵表示。

AES 的处理单位是字节，128 位的输入明文分组 P 和输入密钥 K 都被分成 16 个字节，分别记为 P = P0 P1 … P15 和 K = K0 K1 … K15。如，明文分组为 P = abcdefghijklmnop，其中的字符 a 对应 P0，p 对应 P15。一般地，明文分组用字节为单位的正方形矩阵描述，称为 状态矩阵。在算法的每一轮中，状态矩阵的内容不断发生变化，最后的结果作为密文输出。该矩阵中字节的排列顺序为从上到下、从左至右依次排列，如下图所示：

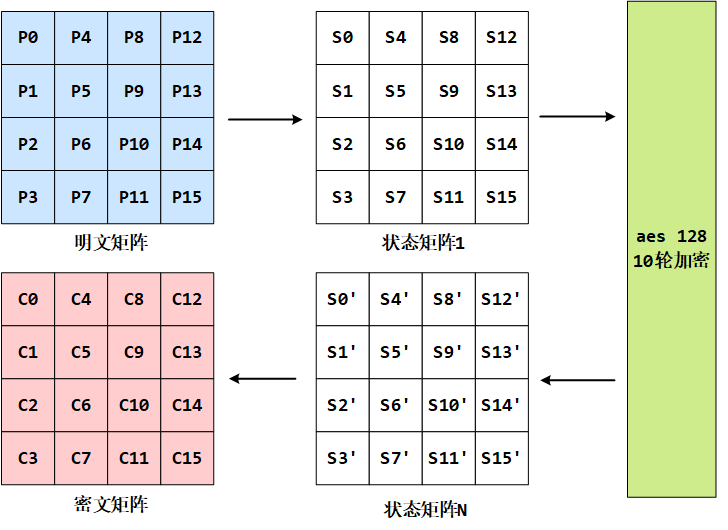
假设明文分组 P 为”abcdefghijklmnop”，则对应上面生成的状态矩阵图如下(此图并未验证数据实际是否是这样，作为参考示例)：

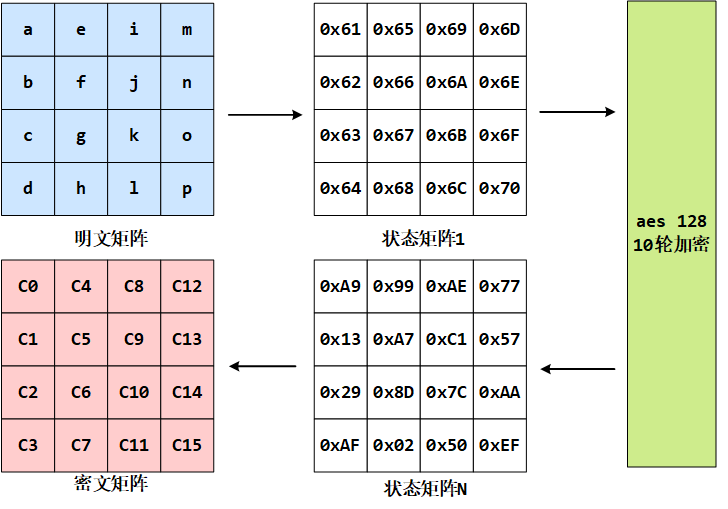
类似地，128 位密钥也是用字节为单位的矩阵表示，矩阵的每一列被称为 1 个 32 位比特字。通过密钥编排函数该密钥矩阵被扩展成一个 44 个字组成的序列 W[0], W[1], … , W[43], 该序列的前 4 个元素 W[0], W[1], W[2], W[3]是原始密钥，用于加密运算中的初始密钥加，后面 40 个字分为 10 组，每组 4 个字（128 比特）分别用于 10 轮加密运算中的轮密钥加，如下图所示：

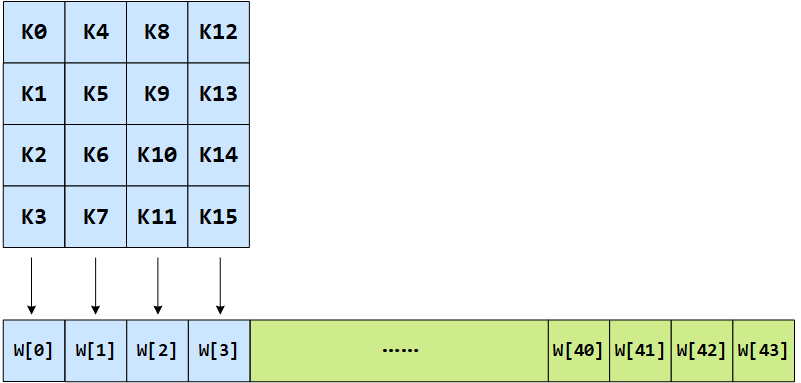
上图中，设 K = “abcdefghijklmnop”，则 K0 = a, K15 = p, W[0] = [K0 K1 K2 K3] = “abcd”。

三、加密步骤分析

伪代码如下：

procedure CIPHER(in, Nr, w) 
    state ← in . See Sec. 3.4 
    state ← ADDROUNDKEY(state,w[0..3]) . See Sec. 5.1.4 
    for round from 1 to Nr - 1 do 
        state ← SUBBYTES(state) . See Sec. 5.1.1 
        state ← SHIFTROWS(state) . See Sec. 5.1.2 
        state ← MIXCOLUMNS(state) . See Sec. 5.1.3 
        state ← ADDROUNDKEY(state,w[4*round..4*round+3])
    end for 
    state ← SUBBYTES(state)
    state ← SHIFTROWS(state)
    state ← ADDROUNDKEY(state,w[4*Nr..4*Nr+3])

    return state . See Sec. 3.4 
end procedure

1. 字节替代(SUBBYTES())变换

字节替代(SUBBYTES())变换是一个非线性的字节替代，它独立地将状态中的每个字节利用替代表(S 盒)进行运算。SUBBYTES()变换在状态上的作用效果如下图：

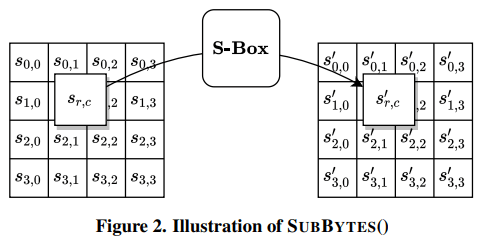
该 S 盒是可逆的，由两个变换复合而成：

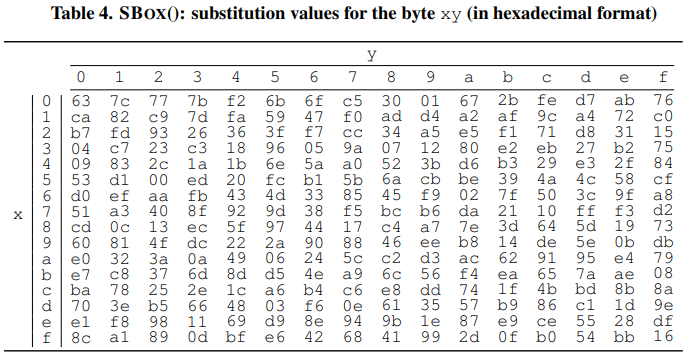
上边的 Table 4 为以 16 进制表示的 SUBBYTES() 变换对应的 S 盒。例如，如果 $S_{1, 1} = 53$ ，则替代后的值将由表中行标为 5，列标为 3 的交集决定。即 $S_{1, 1}^{'} = e d$ 。

根据例子可知状态矩阵中的元素按照下面的方式映射为一个新的字节：把该字节的高 4 位作为行值，低 4 位作为列值，取出 S 盒或者逆 S 盒中对应的行的元素作为输出。例如，加密时，输出的字节 S1 为 0xA9, 则查 S 盒的第 0x0A 行和 0x09 列，得到值 0xD3，然后替换 S1 原有的 0xA9 为 0xD3。状态矩阵经字节代换后的图如下：

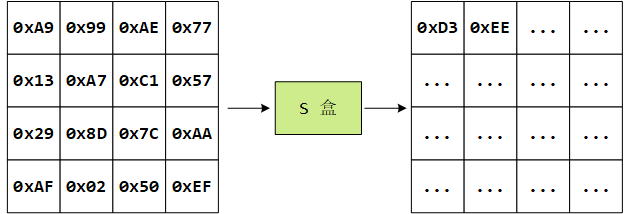
2. 行移位(SHIFTROWS())变换

行移位是一个简单的左循环移位操作。

s_{r, c}^{'} = s_{r, (c + r) m o d 4} f o r 0 \leq r < 4 a n d 0 \leq c < 4

如下图所示：

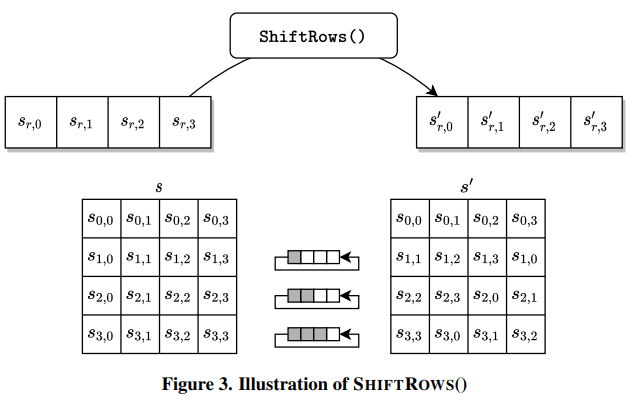
当密钥长度为 128 比特时，状态矩阵的第 0 行左移 0 字节，第 1 行左移 1 字节，第 2 行左移 2 字节，第 3 行左移 3 字节，如下图所示：

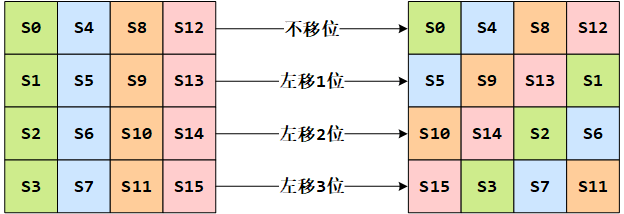
3. 列混合(MIXCOLUMNS())变换

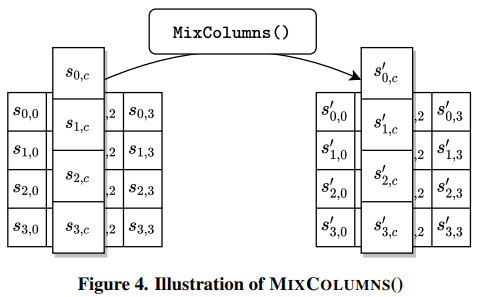
列混合变换是通过矩阵相乘来实现的，经行移位后的状态矩阵与固定的矩阵相乘，得到混合后的状态矩阵，如下公式所示：

[\begin{array}{rrrr} s_{0, c}^{'} \\ s_{1, c}^{'} \\ s_{2, c}^{'} \\ s_{3, c}^{'} \end{array}] = [\begin{array}{rrrr} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{array}] [\begin{array}{rrrr} s_{0, c} \\ s_{1, c} \\ s_{2, c} \\ s_{3, c} \end{array}]

完整的公式为：

[\begin{array}{rrrr} s_{0, 0}^{'} & s_{0, 1}^{'} & s_{0, 2}^{'} & s_{0, 3}^{'} \\ s_{1, 0}^{'} & s_{1, 1}^{'} & s_{1, 2}^{'} & s_{1, 3}^{'} \\ s_{2, 0}^{'} & s_{2, 1}^{'} & s_{2, 2}^{'} & s_{2, 3}^{'} \\ s_{3, 0}^{'} & s_{3, 1}^{'} & s_{3, 2}^{'} & s_{3, 3}^{'} \end{array}] = [\begin{array}{rrrr} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{array}] [\begin{array}{rrrr} s_{0, 0} & s_{0, 1} & s_{0, 2} & s_{0, 3} \\ s_{1, 0} & s_{1, 1} & s_{1, 2} & s_{1, 3} \\ s_{2, 0} & s_{2, 1} & s_{2, 2} & s_{2, 3} \\ s_{3, 0} & s_{3, 1} & s_{3, 2} & s_{3, 3} \end{array}]

状态矩阵中的第 c 列(0 ≤c≤3)的列混合可以表示为下面公式所示：

\begin{aligned} s_{0, c}^{'} & = ({02} \cdot s_{0, c}) \oplus ({03} \cdot s_{1, c}) \oplus s_{2, c} \oplus s_{3, c} \\ s_{1, c}^{'} & = s_{0, c} \oplus ({02} \cdot s_{1, c}) \oplus ({03} \cdot s_{2, c}) \oplus s_{3, c} \\ s_{2, c}^{'} & = s_{0, c} \oplus s_{1, c} \oplus ({02} \cdot s_{2, c}) \oplus ({03} \cdot s_{3, c}) \\ s_{3, c}^{'} & = ({03} \cdot s_{0, c}) \oplus s_{1, c} \oplus s_{2, c} \oplus ({02} \cdot s_{3, c}) \end{aligned}

其中，矩阵元素的乘法和加法都是定义在基于 GF(2^8)上的二元运算, 并不是通常意义上的乘法和加法。这里涉及到一些信息安全上的数学知识，其实这种二元运算的加法等价于两个字节的异或，乘法则复杂一点。对于一个 8 位的二进制数来说，使用域上的乘法乘以(00000010)等价于左移 1 位(低位补 0)后，再根据情况同(00011011)进行异或运算，设 S1 = (a7 a6 a5 a4 a3 a2 a1 a0)，刚 0x02 * S1 如下所示：

(0000 0010) * (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0}) = {\begin{cases} (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0}), a_{7} = 0 \\ (a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0} 0) \oplus (0001 1011, a_{7} = 1 \end{cases}

也就是说，如果 a7 为 1，则进行异或运算，否则不进行。类似地，乘以(00000100)可以拆分成两次乘以(00000010)的运算：

(0000 0100) * (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0}) = (0000 0010) * (0000 0010) * (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0})

乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010)，再将两个乘积异或：

\begin{aligned} (0000 0011) * (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0}) & = [(0000 0010) \oplus (0000 0001)] * (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0}) \\ = [(0000 0010) * (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0})] \oplus (a_{7} a_{6} a_{5} a_{4} a_{3} a_{2} a_{1} a_{0}) \end{aligned}

因此，我们只需要实现乘以 2 的函数，其他数值的乘法都可以通过组合来实现。举个例子：

GF（Galois Field）：伽罗瓦域

4. 轮密钥加(ADDROUNDKEY())变换

轮密钥加是将 128 位轮密钥 Ki 同状态矩阵中的数据进行逐位异或操作。如下图所示。其中，密钥 Ki 中每个字 W[4i], W[4i+1], W[4i+2], W[4i+3]为 32 位比特字，包含 4 个字节。轮密钥加过程可以看成是字逐位异或的结果，也可以看成字节级别或者位级别的操作。也就是说，可以看成 S0 S1 S2 S3 组成的 32 位字与 W[4i]的异或运算。

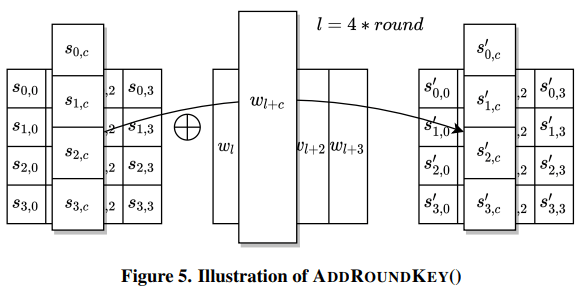
其实就是下图这个样子：

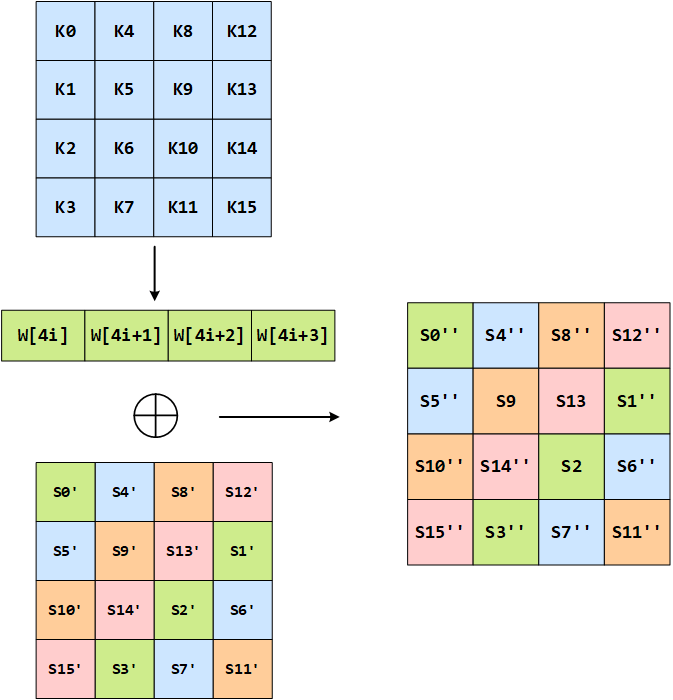
5. 密钥扩展

AES 首先将初始密钥输入到一个 4*4 的状态矩阵中，如下图所示，这个 4*4 矩阵的每一列的 4 个字节组成一个字，矩阵 4 列的 4 个字依次命名为 W[0]、W[1]、W[2]和 W[3]，它们构成一个以字为单位的数组 W。例如，设密钥 K 为”abcdefghijklmnop”, 则 K0 = ‘a’, K1 = ‘b’, K2 = ‘c’, K3 = ‘d’, W [0] = “abcd”：

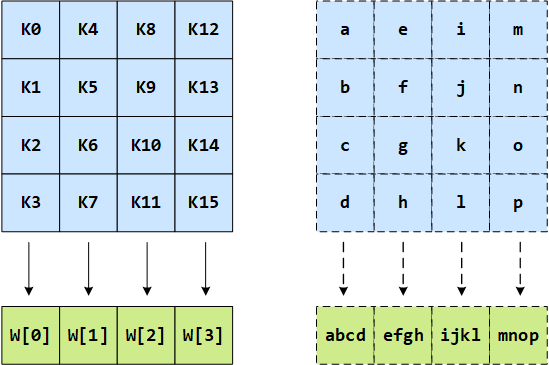
然后，对 W 数组扩充 40 个新列，构成总共 44 列的扩展密钥数组。新列以如下的递归方式产生：

（1）如果 i 不是 4 的倍数，那么第 i 列由 $W [i] = W [i - 4] ⨁ W [i - 1]$ 确定

（2）如果 i 是 4 的倍数，那么第 i 列由等式 $W[i]=W[i-4] \bigoplus T(W[i-1]) $ 确定

其中，T 是一个有点复杂的函数。函数 T 由 3 部分组成：字循环、字节代换和轮常量异或，这 3 部分的作用分别如下。

a.字循环：将 1 个字中的 4 个字节循环左移 1 个字节。即将输入字[b0, b1, b2, b3]变换成[b1, b2, b3, b0]。

b.字节代换：对字循环的结果使用 S 盒进行字节代换。

c.轮常量异或：将前两步的结果同轮常量 Rcon [j] 进行异或，其中 j 表示轮数。

轮常量 Rcon [j] 是一个字，其值见下表。

j	1	2	3	4	5
Rcon [j]	01 00 00 00	02 00 00 00	04 00 00 00	08 00 00 00	10 00 00 00
j	6	7	8	9	10
Rcon [j]	20 00 00 00	40 00 00 00	80 00 00 00	1B 00 00 00	36 00 00 00

举个例子，设初始的 128 位密钥为：3C A1 0B 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD，那么 4 个初始值为：

W[0] = 3C A1 0B 21 
W[1] = 57 F0 19 16 
W[2] = 90 2E 13 80 
W[3] = AC C1 07 BD

下面求扩展的第 1 轮的子密钥( $W [4], W [5], W [6], W [7]$ )。由于 4 是 4 的倍数，所以： $$W[4]=W[0] \bigoplus T(W[3]) $$。 $T (W [3])$ 的计算步骤如下：

（1）循环地将 W[3]的元素移位：AC C1 07 BD 变成 C1 07 BD AC;

（2）将 C1 07 BD AC 作为 S 盒的输入，输出为 78 C5 7A 91;

（3）将 78 C5 7A 91 与第一轮轮常量 Rcon[1]进行异或运算，将得到 79 C5 7A 91，因此，T(W[3])= 79 C5 7A 91，故

W [4] = 3C A1 0B 21 ⨁ 79 C5 7A 91 = 45 64 71 B0

其余的 3 个子密钥段的计算如下：

\begin{aligned} W [5] = W [1] ⨁ W [4] = 57 F0 19 16 ⨁ 45 64 71 B0 = 12 94 68 A6 \\ W [6] = W [2] ⨁ W [5] = 90 2E 13 80 ⨁ 12 94 68 A6 = 82 BA 7B 26 \\ W [7] = W [3] ⨁ W [6] = AC C1 07 BD ⨁ 82 BA 7B 26 = 2E 7B 7C 9B \end{aligned}

所以，第一轮的密钥为 45 64 71 B0 12 94 68 A6 82 BA 7B 26 2E 7B 7C 9B。

密钥扩展伪代码：

procedure KEYEXPANSION(key) 
    i ← 0 
        while i ≤ Nk -1 do 
            w[i] ← key[4 * i..4 * i+3]
            i ← i+1 
    end while    . When the loop concludes, i = Nk. 
    while i ≤ 4*Nr +3 do 
        temp ← w[i-1]
        if i mod Nk = 0 then 
            temp ← SUBWORD(ROTWORD(temp))⊕Rcon[i/Nk]
        else if Nk > 6 and i mod Nk = 4 then 
            temp ← SUBWORD(temp)
        end if 
        w[i] ← w[i-Nk]⊕temp
        i ← i+1 
    end while 
    return w
end procedure

四、解密步骤分析

将加密变换逆转，然后以逆序执行即可直接得到解密算法。解密算法伪代码：

procedure INVCIPHER(in, Nr, w) 
    state ← in . See Sec. 3.4 
    state ← ADDROUNDKEY(state,w[4*Nr..4*Nr+3]) . See Sec. 5.1.4 
    for round from Nr -1 downto 1 do 
        state ← INVSHIFTROWS(state) . See Sec. 5.3.1 
        state ← INVSUBBYTES(state) . See Sec. 5.3.2 
        state ← ADDROUNDKEY(state,w[4*round..4*round+3])
        state ← INVMIXCOLUMNS(state) . See Sec. 5.3.3 
    end for 
    state ← INVSHIFTROWS(state)
    state ← INVSUBBYTES(state)
    state ← ADDROUNDKEY(state,w[0..3])
    return state
end procedure

1. 逆行移位(INVSHIFTROWS())变换

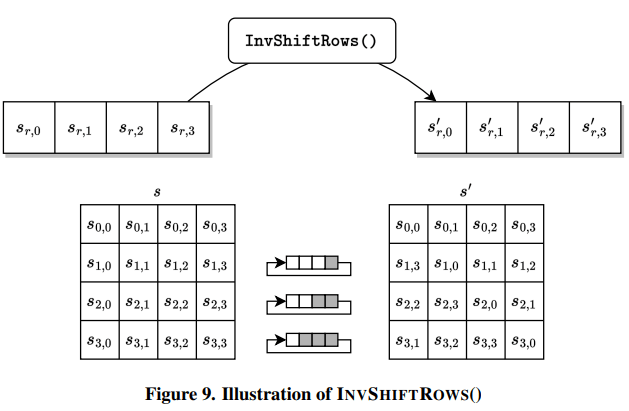
2. 逆字节替代(INVSUBBYTES())变换

逆字节替代(INVSUBBYTES() )变换是字节替代(SUBBYTES())变换的逆变换，在状态的每个字节上应用 S 盒的逆。

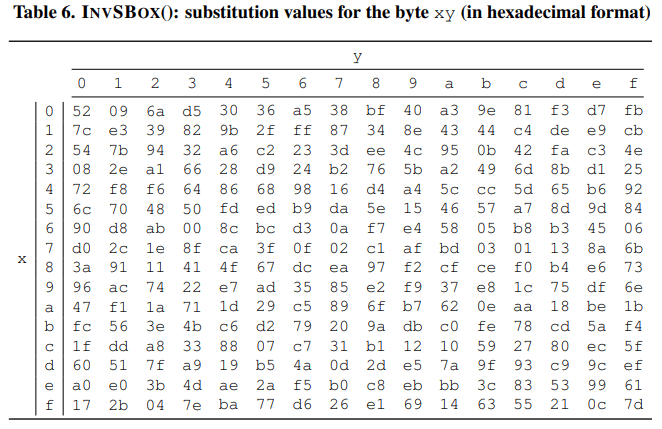
3. 逆列混合(INVMIXCOLUMNS())变换

逆列混合(INVMIXCOLUMNS())变换是列混合(MIXCOLUMNS())变换的逆变换。

[\begin{array}{rrrr} s_{0, c}^{'} \\ s_{1, c}^{'} \\ s_{2, c}^{'} \\ s_{3, c}^{'} \end{array}] = [\begin{array}{rrrr} 0 e & 0 b & 0 d & 09 \\ 09 & 0 e & 0 b & 0 d \\ 0 d & 09 & 0 e & 0 b \\ 0 b & 0 d & 09 & 0 e \end{array}] [\begin{array}{rrrr} s_{0, c} \\ s_{1, c} \\ s_{2, c} \\ s_{3, c} \end{array}] f o r 0 \leq c < 4

经过该乘法计算后，一列中的 4 个字节将由下述结果取代：

\begin{array}{r} s_{0, c}^{'} = ({0 e} \cdot s_{0, c}) \oplus ({0 b} \cdot s_{1, c}) \oplus ({0 d} \cdot s_{2, c}) \oplus ({09} \cdot s_{3, c}) \\ s_{1, c}^{'} = ({09} \cdot s_{0, c}) \oplus ({0 e} \cdot s_{1, c}) \oplus ({0 b} \cdot s_{2, c}) \oplus ({0 d} \cdot s_{3, c}) \\ s_{2, c}^{'} = ({0 d} \cdot s_{0, c}) \oplus ({09} \cdot s_{1, c}) \oplus ({0 e} \cdot s_{2, c}) \oplus ({0 b} \cdot s_{3, c}) \\ s_{3, c}^{'} = ({0 b} \cdot s_{0, c}) \oplus ({0 d} \cdot s_{1, c}) \oplus ({09} \cdot s_{2, c}) \oplus ({0 e} \cdot s_{3, c}) \end{array}

4. 轮密钥加(AddRoundKey())变换的逆变换

轮密钥加(AddRoundKey())变换，其逆变换就是它本身，因为其中只应用了异或(XOR)运算。

5. 等价的解密变换

AES 算法流程一节中的图，所描述的直接得到的解密算法中，其各个变换的操作顺序与加密算法不同，伪代码对比如下：

但是加密和解密算法中的密钥编排形式相同。然而，AES 算法的若干性质允许构造一个等价的解密算法，解密时各个变换的操作顺序与加密(由逆变换取代原来的变换)相同。这是通过改变密钥编排完成的。

允许该等价解密变换的两个关键性质如下：

（1）字节替代(SubBytes())变换和行移位(ShiftRows())变换的顺序不影响结果。即，先进行字节替代(SubBytes())变换紧接着进行行移位(ShiftRows())变换等价于先进行行移位(ShiftRows())变换紧接着再进行字节替代(SubBytes())变换。对于逆变换 InvSubBytes()和 InvShiftRows()，该性质也成立。
（2）列混合运算－MixColumns()和 InvMixColumns()－是关于列输入的线性变换，即意味着 InvMixColumns(state XOR Round Key)＝ InvMixColumns(state) XOR InvMixColumns(Round Key)。

这些性质使得 InvSubBytes()变换和 InvShiftRows()变换可以交换顺序。AddRoundKey ()变换和 InvMixColumns()变换的顺序也可以交换，只要将解密中密钥编排得到的密钥列（字）应用 InvMixColumns()变换进行修改即可。

等价的解密算法伪代码如下所示：

// Algorithm 4 Pseudocode for EQINVCIPHER() 
procedure EQINVCIPHER(in, Nr, dw) 
    state ← in
    state ← ADDROUNDKEY(state,dw[4*Nr..4*Nr+3])
    for round from Nr-1 downto 1 do 
        state ← INVSUBBYTES(state)
        state ← INVSHIFTROWS(state)
        state ← INVMIXCOLUMNS(state)
        state ← ADDROUNDKEY(state,dw[4* round..4*round +3])
    end for 
    state ← INVSUBBYTES(state)
    state ← INVSHIFTROWS(state)
    state ← ADDROUNDKEY(state,dw[0..3])
    return state
end procedure

// Algorithm 5 Pseudocode for KEYEXPANSIONEIC()
procedure KEYEXPANSIONEIC(key) 
    i ← 0 
    while i ≤ Nk-1 do 
        w[i] ← key[4i..4i+3]
        dw[i] ← w[i]
        i ← i+1 
    end while . When the loop concludes, i = Nk. 
    while i ≤ 4*Nr +3 do 
        temp ← w[i-1]
        if i mod Nk = 0 then 
            temp ← SUBWORD(ROTWORD(temp))⊕Rcon[i/Nk]
        else if Nk > 6 and i mod Nk = 4 then 
            temp ← SUBWORD(temp)
        end if 
        w[i] ← w[i-Nk]⊕temp
        dw[i] ← w[i]
        i ← i+1 
    end while 
    for round from 1 to Nr-1 do 
        i ← 4*round
        dw[i..i+3] ← INVMIXCOLUMNS(dw[i..i+3]) . Note change of type. 
    end for 
    return dw
end procedure

基本流程图如下：

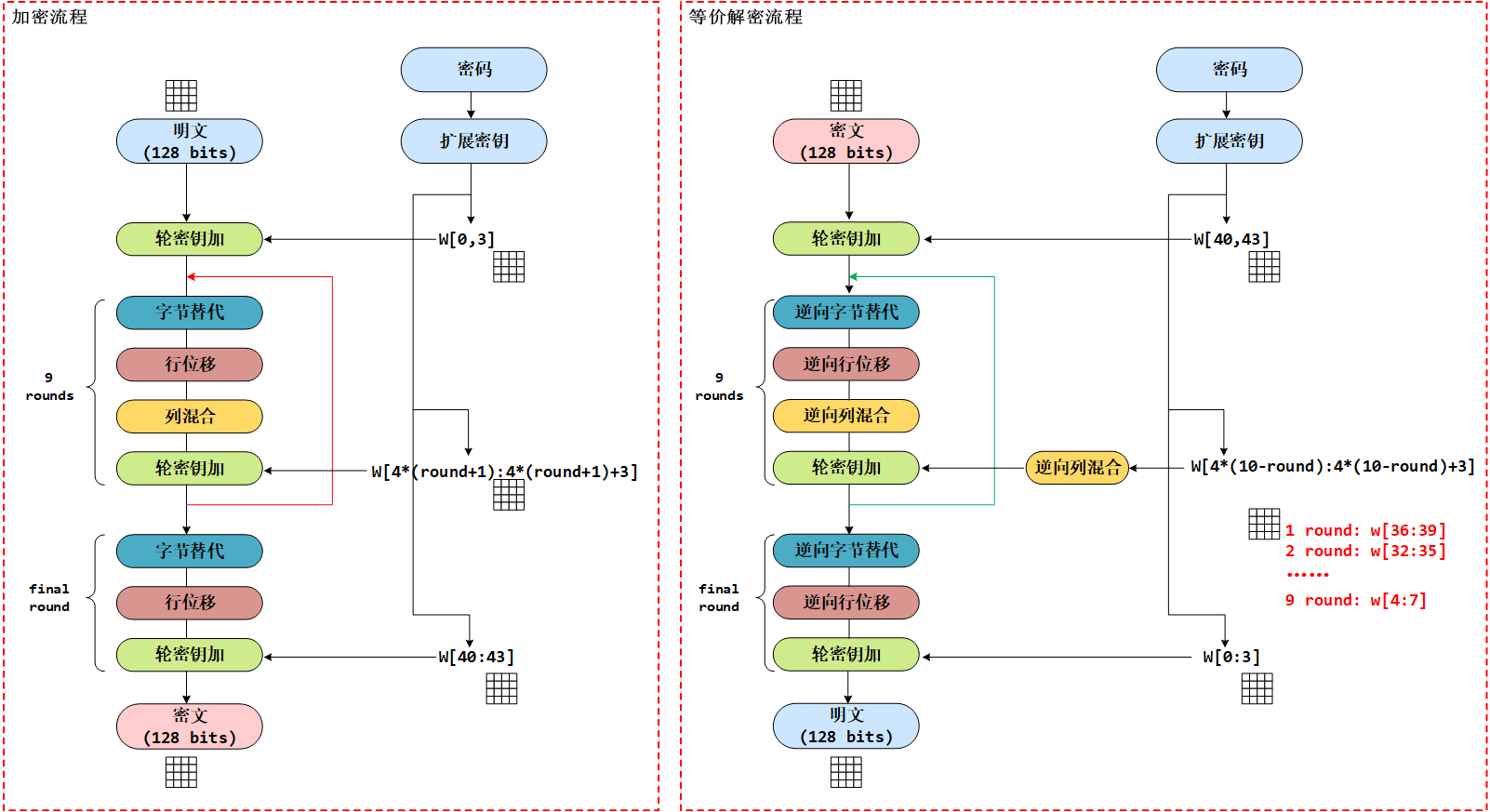
参考资料：
xilinx.github.io/Vitis_Libraries/security/2020.1/guide_L1/internals/aes.HTML
AES 加密算法原理的详细介绍与实现-CSDN 博客
高级加密标准 AES-FIPS197 中文版 - 道客巴巴

LV015-AES基本原理 ​

一、基础知识 ​

1. 输入和输出 ​

2. 状态(State) ​

3. 加解密函数 ​

二、AES-128 算法流程 ​

三、加密步骤分析 ​

1. 字节替代(SUBBYTES())变换 ​

2. 行移位(SHIFTROWS())变换 ​

3. 列混合(MIXCOLUMNS())变换 ​

4. 轮密钥加(ADDROUNDKEY())变换 ​

5. 密钥扩展 ​

四、解密步骤分析 ​

1. 逆行移位(INVSHIFTROWS())变换 ​

2. 逆字节替代(INVSUBBYTES())变换 ​

3. 逆列混合(INVMIXCOLUMNS())变换 ​

4. 轮密钥加(AddRoundKey())变换的逆变换 ​

5. 等价的解密变换 ​