LV020-透镜成像
这一节来看一下透镜和成像公式。
一、透镜简介
1. 什么是透镜
透镜是由至少一面或多面曲面(通常为球面或非球面)构成的透明介质(常用玻璃或塑料)光学元件,它能使通过的光线发生折射,使光线发生聚合或发散,从而在一定条件下形成实像或虚像。
在前面,我们利用小孔进行成像,当光线透过小孔后,将会在传感器上投影出倒立的实像。然而,由于隔板阻挡了物体反射的绝大部分光线,将导致投影出的实像并不是很清晰。为了弥补小孔成像的不足,我们由凸透镜来代替小孔,使之成为光线的汇聚组件:
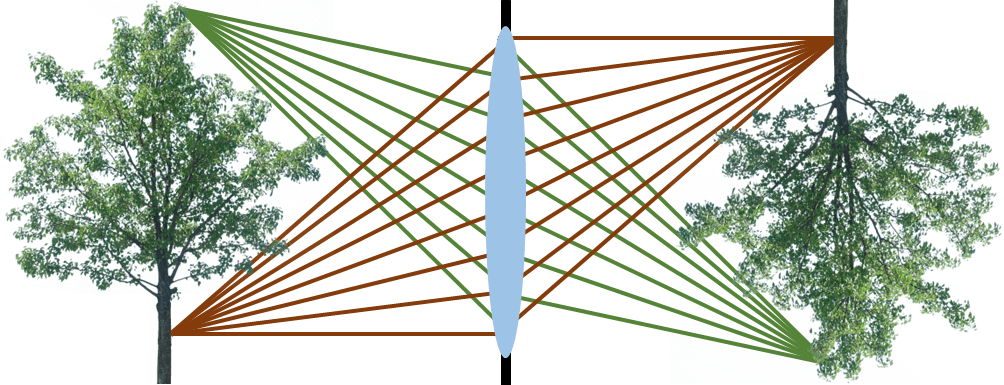
上图利用凸透镜进行成像,我们可以发现:物体上一个点所反射的光线将被凸透镜汇聚在传感器上的一个点。凸透镜能够汇聚物体的反射的光线在某点投影,而不是像小孔一样隔开大部分的光线,因此凸透镜成像将会比小孔成像更加清晰。正是因为凸透镜成像的优势,现代相机都采用凸透镜进行成像,采用凸透镜的相机也被称为现代光学相机。
2. 凸透镜与凹透镜
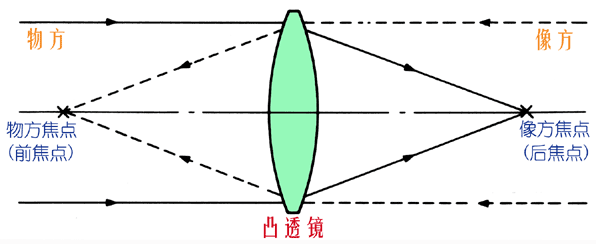
凸透镜(正透镜):中央部分比边缘厚,可将平行入射光线会聚到一点(焦点)。对于成像用途,我们最关心的是凸透镜的成像特性,因为凸透镜能在成像平面上得到倒立、缩小或放大的实像。
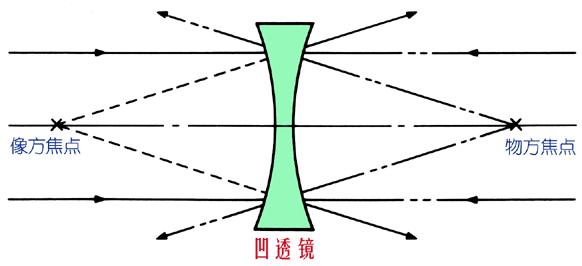
凹透镜(负透镜):中央较薄、边缘较厚,将平行入射光线发散开,不适用于直接在感光平面上形成实像。凹透镜常用于矫正像差或与凸透镜组合成复合镜头系统,但单独的凹透镜不能在屏幕上成实像。
3. 焦点
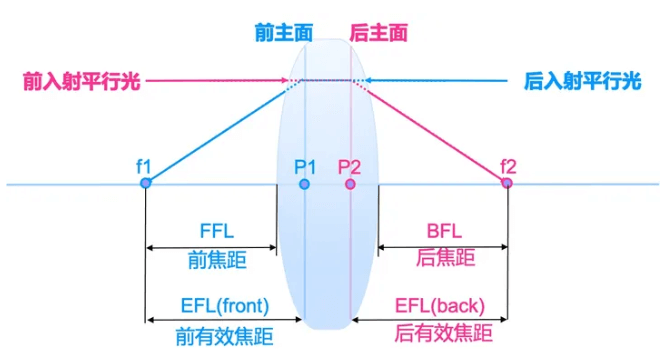
所谓“光轴”就是一条垂直穿过理想透镜中心的光线。当一束平行于透镜光轴的光线射入凸透镜后,这束平行光线会在透镜另一侧会聚于一点,这个点就是透镜的焦点(focal point、focus)。
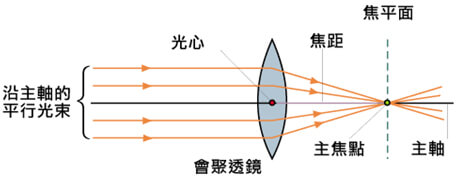
在光学术语上,以透镜为界:被摄物体所在的空间称为“物方空间”;被摄物体所发出的光穿越透镜在透镜后面形成的像所在的空间称为“像方空间”;在像方空间所形成的焦点称为“像方焦点”或“后焦点”;反之,从像方开始,投射出与光轴平行的光线,并在透镜物体空间所形成的焦点,称为“物方焦点”或“前焦点”。
 |  |
4. 焦距
一个透镜的轴向厚度与其直径、物距、像距以及焦距相比显得很小,就可以认为该透镜是 薄透镜。一片薄的双凸透镜的 焦点距离(一般用 f 表示),一般指透镜光学中心(通常定义透镜的主光学平面)到焦点为止的光轴上的距离,这个镜片的中心叫做“主点”。焦距是透镜最重要的光学参数之一,它取决于透镜的材质折射率和曲率半径。
焦距越短,透镜的会聚能力越强;焦距越长,透镜会聚光线的能力越弱。
但是实际的镜头都是由数片凸透镜和凹透镜组合而成,无法直接分辨出主点的位置。但是具体的内容就不是这里学习的重点了,暂时了解到这里。这里放张图大概看一下:
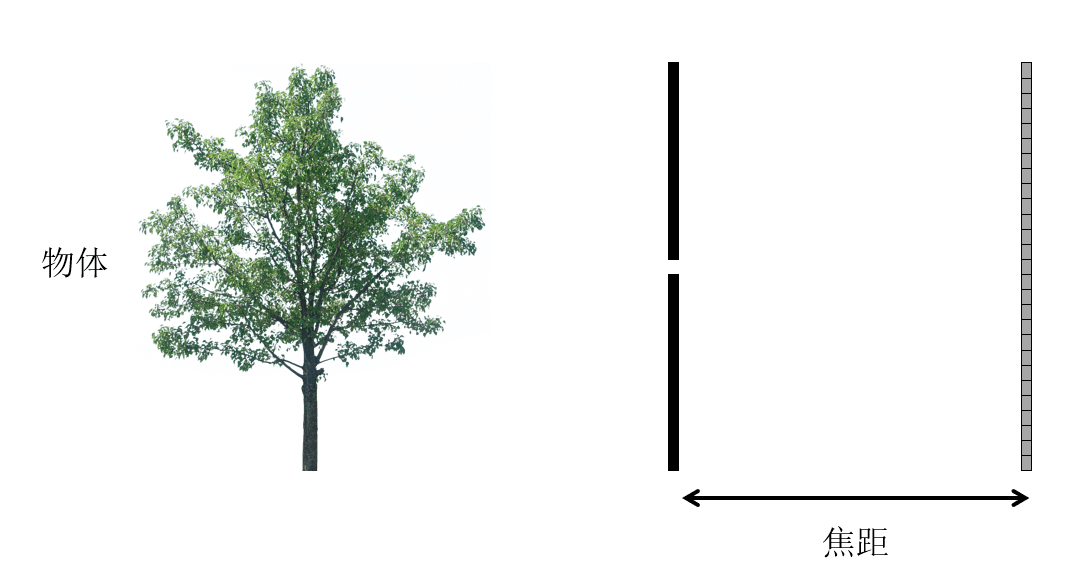
要是按照上面小孔成像,那就是隔板与传感器平面之间的距离就称为焦距。
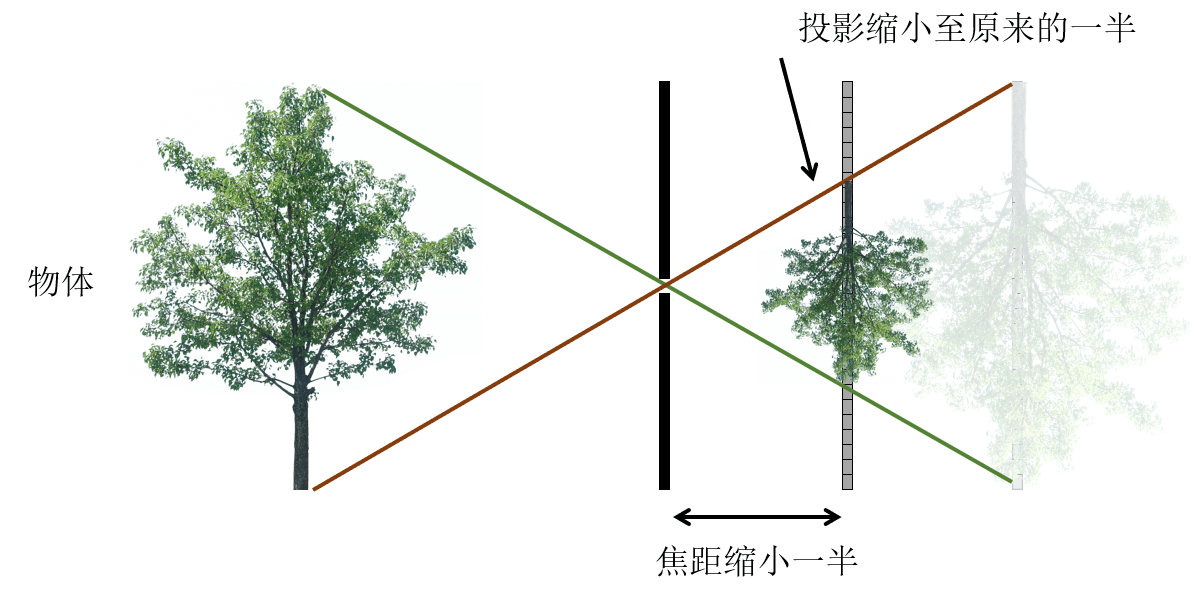
当我们保持物体与隔板之间的距离不动,并缩小传感器与隔板之间的距离时,就发生了有趣的现象:当焦距缩短一半时,成像的尺寸大小也会缩小一半;当焦距扩大一倍时,成像的尺寸大小也会扩大一倍。如下图所示:
5. 视场角
在光学镜头领域,我们经常会听到这样一个词,视场角],即 Field of view(FOV),视场角又称视场,它的大小决定了光学仪器的视野范围。在光学仪器中,以光学仪器的镜头为顶点,以被测目标的物像可通过镜头的最大范围的两条边缘构成的夹角,称为视场角。
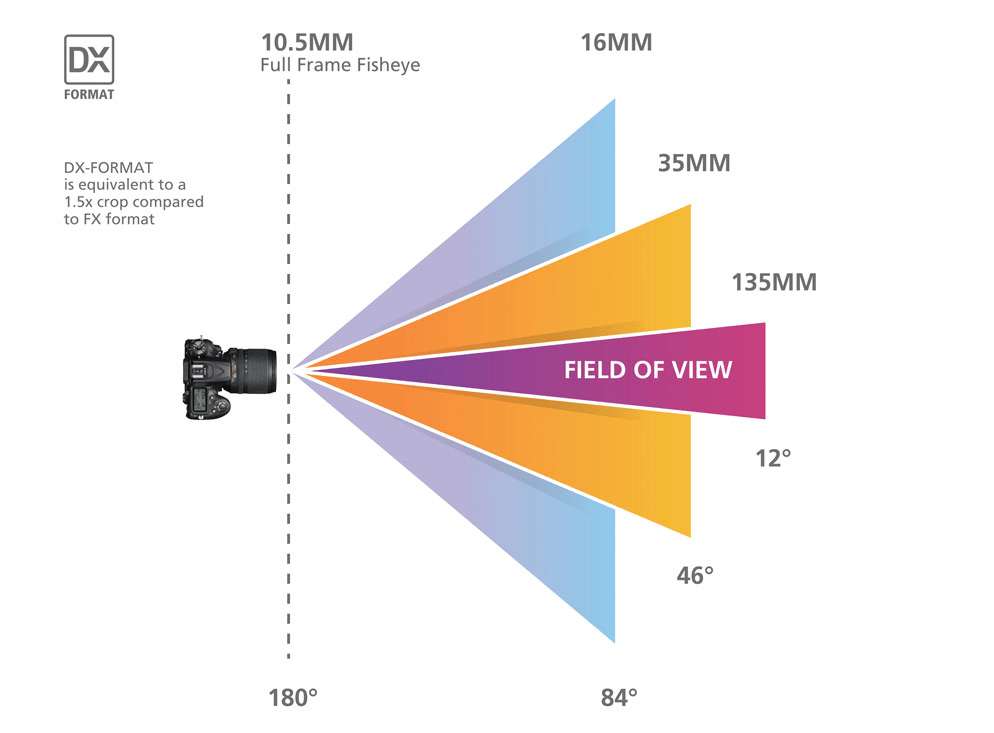
视场角,与两件事有关,镜头的 焦距 以及 图像传感器的尺寸。假定镜头焦距相同,图像传感器的尺寸越大,视场角也就越大,反之亦然。
镜头的焦距表示镜头与图像传感器上聚焦图像之间的距离。当光通过镜头时,它要么会聚集 (正焦距),要么会发散(负焦距),但在相机内,焦距主要是正的。焦距的距离决定了镜头汇聚光线的强度,同时也会影响到捕捉光线的水平角度。这里要提出一个概念,固定视场角(AFOV),是指在水平方向捕获的任何光线与在边缘捕获的任何光线之间的角度。如果图像传感器的尺寸不变,改变焦距将改变 AFOV,从而改变整体 FOV。更短的焦距提供更大的 AFOV 视图,也能提供更大的 FOV。
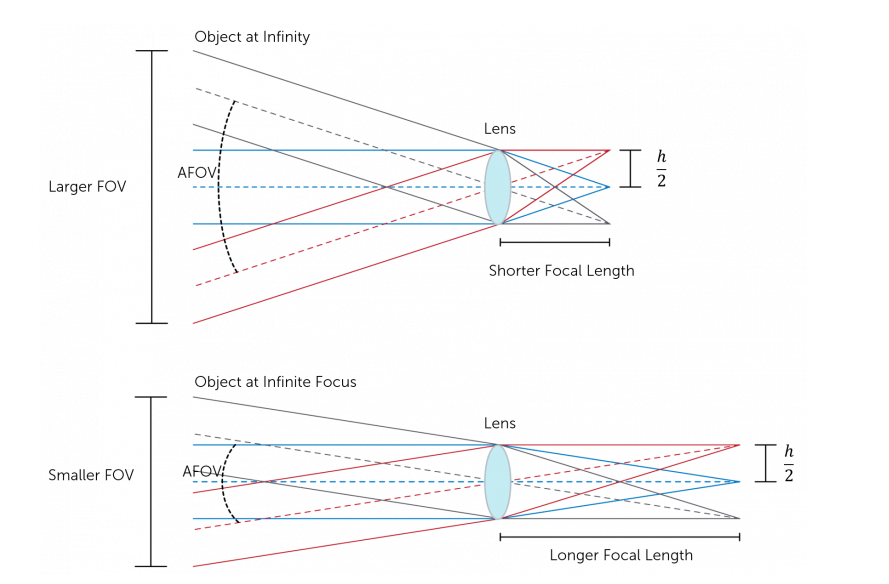
总的来说就是图像传感器尺寸一定的情况下,焦距越短,视场角越大,下图是一个示例,但具体的其实还是要看镜头的手册。
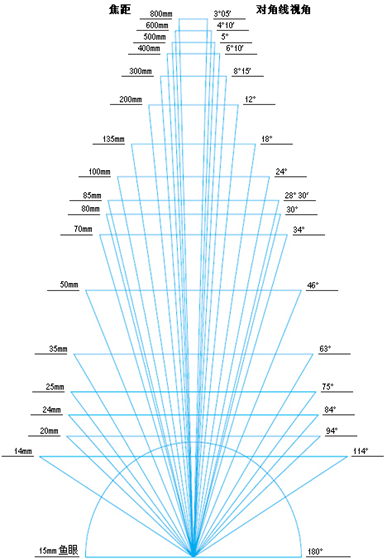
二、成像公式
1. 成像公式的基本形式
高斯成像公式在薄透镜近轴光学假设下(即忽略高阶像差与仅考虑光轴附近小角度光线)成立。公式为:
其中 f 为透镜焦距,u 为物距,即物体到透镜光学中心的距离,v 为像距,即透镜到成像平面的距离(像平面与透镜之间的距离)
2. 近轴近似与理想透镜
高斯成像公式成立的前提是所谓的“近轴近似”条件:
- 光线接近光轴传播,即光线入射角度很小,不考虑大量像差。
- 透镜薄到可以将其光学属性集中在一个单一平面上,不考虑透镜厚度 带来的光线偏移。
- 在此条件下,光路可以用几何光学简单的折射定律来分析,得到简单的代数关系。
3. 怎么推导?
推导高斯成像公式通常从相似三角形与折射定律出发
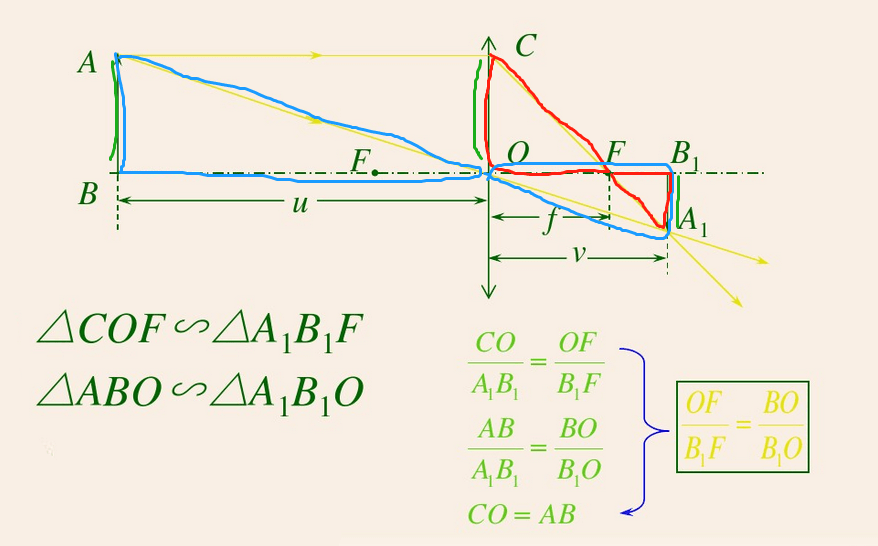
4. 成像性质
这里有一个在线演示的网站:几何光学
| 物的位置 | 像的位置 | 像的性质 | 应用 |
|---|---|---|---|
| 无限远 | 像物异侧(像和物体分别处于凸透镜的两侧),v = f | 成一点 | / |
| u > 2f | 像物异侧,2f > v > f | 倒立、缩小、实像 | 照相机 |
| u = 2f | 像物异侧,v = 2f | 倒立、等大、实像 | 计算焦距 |
| 2f > u > f | 像物异侧,v > 2f | 倒立、放大、实像 | 投影仪、显微镜的物镜 |
| u = f | 不成像 | 不成像 | 不成像 |
| u < f | 像物同侧,v > u | 正立、放大、虚像 | 放大镜,显微镜的目镜 |
5. 成像放大率
成像公式还可与放大率概念结合:放大率 m 定义为像高与物高的比值,也等同于像距和物距的比值(在近轴近似下):
对于相机而言,为了拍摄清晰的微距影像,物体距离相对较小,就会使像距增加,从而放大率上升。
三、实际应用与操作
1. 对焦机制
相机通过移动透镜组或感光平面来改变 v ,使得对给定的 u(物体位置)满足成像公式,从而在感光传感器上形成清晰的像。如果物体还远近变化,相机就需要重新调整镜头焦距或镜头到感光面的距离(在定焦镜头中是移动镜头或者传感器位置,在变焦镜头中可改变有效焦距)来再次满足成像公式。
2. 固定焦距镜头与变焦镜头
固定焦距镜头:焦距 f 是固定的,通过改变镜头与传感器间距离(微小调焦)来满足不同比例的 u 和 v,以确保对焦。
变焦镜头:可通过内部透镜组间距变化改变 f ,从而在不同焦距下对物体成像,再由微调对焦来准确满足公式。
3. 拍摄场景下的直观理解
当对一个比较远的物体对焦时,物距 u 非常大,$\frac{1}{u} $ 几乎为 0,因此像距 v 接近 f 。相机聚焦到无穷远时,其感光面平面几乎固定在 f 处。
当试图拍摄较近的物体,如微距拍摄,u 减小,
参考资料:
焦点与焦距 (focal point, focal length)-CSDN 博客