LV012-G711基本原理
一、G711 压扩算法
G711 算法采用 8kHz 采样率,有 A-law 和 μ-law 两种压扩方式,分别是将 13bit 和 14bit 编码为 8bit,因此 G711 固定码率是 8kHz x 8bit = 64kbps。两者都是对数变换,A-law 更加方便计算机处理。μ-law 提供了略微高一些的动态范围,但代价是对于弱信号的量化误差相对 A-law 高一些。两者均采用对数变换的原因也正是由于人耳对于声音的感知不是线性变化而是对数型变化的特性。
1. A-law
A-law 的公式如下,一般采用 A = 87.6:
画出图来则是如下图,用 x 表示输入的采样值,F(x)表示通过 A-law 变换后的采样值,y 是对 F(x)进行量化后的采样值。
由此可见在输入的 x 为高值的时候,F(x)的变化是缓慢的,有较大范围的 x 对应的 F(x)最终被量化为同一个 y,精度较低。相反在低声强区域,也就是 x 为低值的时候,F(x)的变化很剧烈,有较少的不同 x 对应的 F(x)被量化为同一个 y。意思就是说在声音比较小的区域,精度较高,便于区分,而声音比较大的区域,精度不是那么高。
2. μ-law
μ-law 的公式如下,μ 取值一般为 255
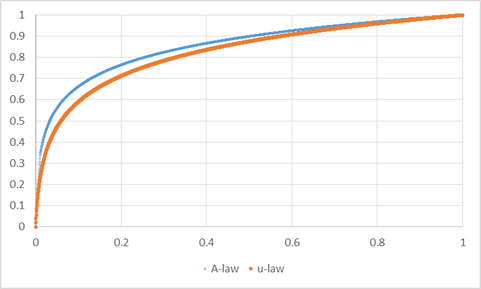
和 A-law 画在同一个坐标轴中就能发现 A-law 在低强度信号下,精度要稍微高一些。
二、折线近似
我们确实可以用浮点数计算的方式把 F(x)结果计算出来,然后进行量化,但是这样一来计算量会比较大,实际上对于 A-law(A = 87.6 时),是采用 13 折线近似的方式来计算的,而 μ-law(μ = 255 时)则是 15 段折线近似的方式。
1. 数学原理
以 A-law 为例来看一下:
A = 87.6 时,函数图像接近原点,函数图像如下:
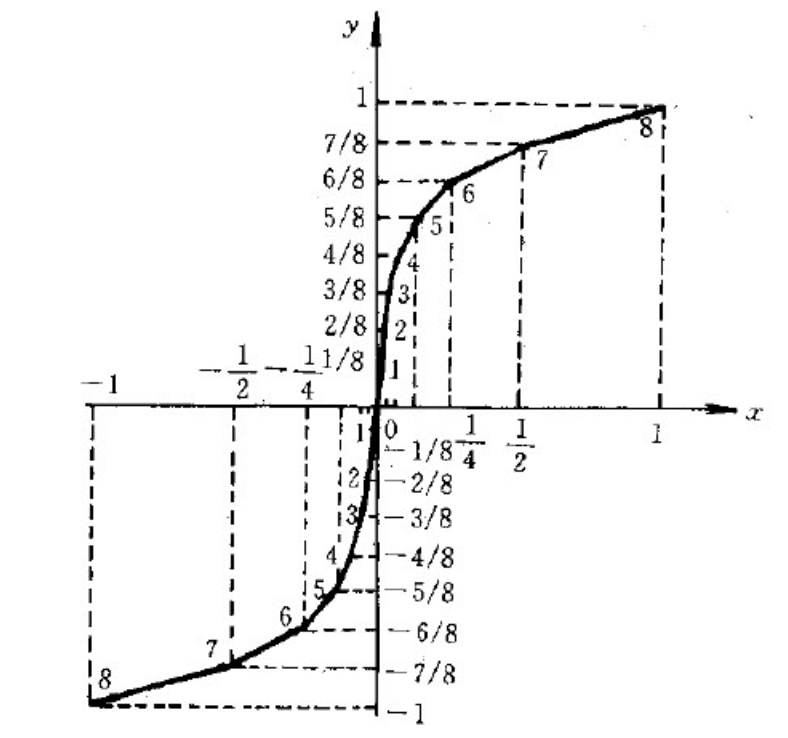
该函数图中,X 表示输入信号,Y 表示输出信号,且均归一化到(-1, +1)区间;将 x 轴(0,1)非均匀量化为为 8 段 1/2、1/4、… 1/64、1/128 最终到原点 0,共 8 段;同理每段对应到 Y 轴上也有 8 段,并且 x 负轴也分为这相同的 8 段,在原点(0,0)处,-1/64 到+1/64 是实质是相同的斜率,可归纳一个段,加上剩余的 12 段,也就是十三段,经过十三折线后的函数图像不再像上图的曲线,而是一段段的直线连接,折线图逼近 A-law 曲线图,故称 十三折线法;并且十三段折线对应不同的斜率,在值较小时,曲线斜率近似于折线,精度较高,而值较大时,则曲线斜率与折线相差较大,精度较低。
在以上基础上,我们将每一个(如 1-1/2、1/2-1/4)大段称为“段落”,在每个段落内部实现均分 16 分,这样在 X 轴上(-1,+1)就有 16 个段落 * 16 个均分 = 256 个量级;对应到 Y 轴上也是 256 个量级,这样我们就将输入信号编码离散化到 256 个量级范围,刚好是 8Bit,也就是编码后的值范围在 256 量级,也就是 8Bit;而输入端 X,我们段落之间非均匀化划分,段内 16 分均匀划分,这种均匀-非均匀量化范围可以 0~2048(12bit)的范围,加上还有负数的情况(1bit 极性),所以我们输入信号可以对 13bit 的数据进行编码,按照这种原理进行量化的表格如下:
| 量化范围 | 归一化 | 段落码(3bit) | 权重值 |
|---|---|---|---|
| 0~16 | 0~1/128 | 0 0 0 | 8 4 2 1 |
| 16~32 | 1/128~1/64 | 0 0 1 | 8 4 2 1 |
| 32-64 | 1/64~1/32 | 0 1 0 | 16 8 4 2 |
| 64~128 | 1/32~1/16 | 0 1 1 | 32 16 8 4 |
| 128~256 | 1/16~1/8 | 1 0 0 | 64 32 16 8 |
| 256~512 | 1/8~1/4 | 1 0 1 | 128 64 32 16 |
| 512~1024 | 1/4~1/2 | 1 1 0 | 256 128 64 32 |
| 1024~2048 | 1/2~1 | 1 1 1 | 512 256 128 64 |
总段落实质是 16 个段落,8 个正 8 个负,负数情况下转为正进行查表,同时记录正负极性。而段内码是均匀划分,表格如下:
| 量化范围 | 段内码(4bit) |
|---|---|
| 0 | 0x0 |
| 1 | 0x1 |
| 2 | 0x2 |
| ... | ... |
| 15 | 0xf |
拥有上面两张表后,我们就可以实现对输入信号进行编码压缩了,上面段落码+段内码一共才 7bit,还差一位 bit,这个就是信号的极性,正负了;
例如,输入信号 2000,输出编码是多少?
(1)确定段落码:2000 在 1024~2048 段,所以段落码是 1 1 1
(2)确定段内码:2000 - 1024 = 976,1024~2048 段内权重值为 512 256 128 64,也就是 512*x + 256*y+128*z + 64*w 趋近于 976,最终 x = 1,y = 1,z = 1,w = 1;
(3)极性取反 2000 的符号位是 0,所以极性为 1
最终 2000 的编码值为 1 1 1 1 1 1 1 1 = 0xff。
2. 算法实现
前面是十三折线法原理,但是转化到计算机上来还是有区别的,例如我们一般存储数据类型都是 8 的倍数类型存储,如 short 类型就是 16bit,但是十三折线是针对 13bit 的数据压缩,这个时候就需要自行处理,移除低位 3bit 或者高位 3bit,根据自己的需求处理。
并且计算机处理做了特殊的改动,A-law 如下表计算,第一列是采样点,共 13bit,最高位为符号位。对于前两行,折线斜率均为 1/2,跟负半段的相应区域位于同一段折线上,对于 3 到 8 行,斜率分别是 1/4 到 1/128,共 6 段折线,加上负半段对应的 6 段折线,总共 13 段折线,这就是所谓的 A-law 十三段折线法
- Linear Input code 代表输入的十三 bit 信号值,s 是符号位 0…1 代表序号位,abcd 代表强度位,x 是会移除的 bit。
- Compressed code 是经过压缩编码后的数据,s 取反,0…1 表示输入的序号位,高位第一个 1 的位置,abcd 则是输入保留下来的。
- Linear output code 是逆过程,解码后的数据,s 恢复,abcd 恢复,输入 x 则只会添 1 做补偿,其他为 0,这块也就是误差值存在。
所以,按照上述表格,进行编码的步骤:
(1)获取符号位。
(2)确定序号位的第一个高位 1 的位置,并确定序号编码。
(3)获取强度为 abcd,也就是序号位后紧跟的 4bit。
(4)最后还需要进行异或处理。
参考资料:
G711 原理详解与 A-Law 与 μ-Law 编码算法对比-CSDN 博客